【算法】图论算法

图的基本表示方法已经在搜索算法那一节讲过了，在开头补充一个本节要用到的概念-度

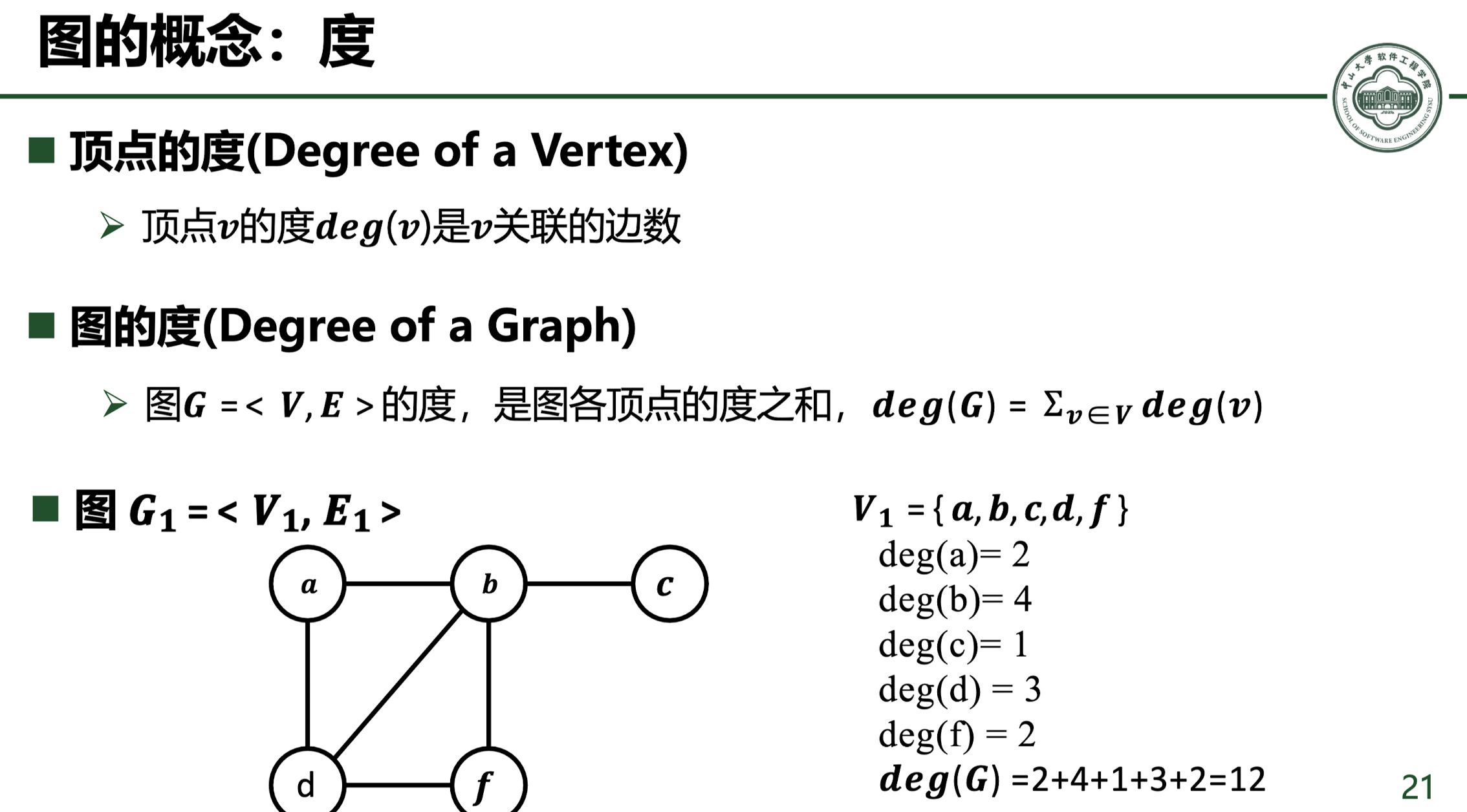
对于无向图，一个点的度就是与这个点关联的边的个数，而对于有向图，分为出度和入度，出度就是离开这个点的边数，入度就是流入这个点的边数。

握手定理：各点度数之和等于边数的两倍。即对 $n$ 阶 $m$ 条边的图有

$$ \sum_i^nd(v_i) = 2m $$

接下来是常见的图论算法

拓扑排序

基本概念

拓扑排序是基于有向无环图的一种关联排序算法，经过拓扑排序后的序列，对于所有的有向边和对应的节点 u->v ，都有点 u 排序在点 v 的后面。

eg

拓扑排序不是唯一的，而且只要存在环就不存在拓扑排序，$n$ 个节点的有向无环图中，最多存在 $n!$ 个拓扑排序（离散点无边的情况），最少有 $1$ 种拓扑排序（完全有序的情况）。

算法流程

拓扑排序的算法是基于图的度来进行的，基本的思想就是对于入度为 0 的点，就可以直接放到序列里，放到序列之后，将这个点的所有出边都删掉，然后又会产生新的入读为 0 的点。重复以上步骤直到所有点都被加入到序列当中。

如果算法过程中存在一个点没有加入，就说明这个图中存在环。

如下图中，点 B, D, H 的入读为 0，加入点 B, D, H，然后将这三个点的和他们关联的所有边删掉，这个时候就会产生新的入度为 0 的点 A, C, G, I，然后删掉，重复这个过程。

具体代码实现可以维护一个数组去存储每个边 u->v，其中edge[u] = v，然后再开一个队列，将入度为 0 的点推入队列，删边的时候一个个取出来就可以了。

例题

这道题有个要求就是编号小的队伍在前面，解决方法就是再加入队列的时候，每次选择字典序较小的编号，优先推入队列，使用小根堆即可。删边时，如果发现删掉后，那个点的入度为 0，就把他加入小根堆。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<iostream>
#include<vector>
#include<queue>
#include<functional>
using namespace std;
const int MAXN = 500;
vector<int> edge[MAXN];
int n,m;
int res[MAXN],degree[MAXN];
priority_queue<int,vector<int>,greater<int>> que;

void Toposort(){
    int rear = 0;
    for(int i=1;i<=n;i++){
        if(degree[i]==0){
            que.push(i);
        }
    }
    while(!que.empty()){
        int x = que.top();
        que.pop();
        res[++rear] = x;
        for(int y:edge[x]){
            if(--degress[y]==0){
                que.push(y);
            }
        }
    }
    cout<<res[1];
    for(int i=2;i<=n;i++){
        cout<<" "<<res[i];
    }
    cout<<endl;
}

int main(){
    while(cin>>n>>m){
        // 重置边集
        for(int i=0;i<MAXN;i++){
            edge[i].clear();
        }
        int u,v;
        for(int i=1;i<=m;i++){
            cin>>u>>v;
            edge[u].push_back(v);
            degree[v]++;
        }
        Toposort();
    }
    return 0;
}

欧拉路与欧拉回路

基本概念

  • 欧拉路：经过图中所有边恰好一次的通路
  • 欧拉回路：经过所有边恰好一次的回路

欧拉回路的判别方法：

对于无向图，存在欧拉回路的充要条件是所有点是连通的且所有点的度数都是偶数。

对于有向图，存在欧拉回路的充要条件是所有点是强连通的（任意两点可达）且每个点的出度与入度相同。

欧拉路的判别方法：

对于无向图，存在欧拉路的充要条件是所有点是连通的且度数为奇数的点恰好存在 0 个或者 2 个。

对于有向图，存在欧拉路的充要条件是所有点是连通的且最多只有一个点出度比入度大 1，另一个点入度比出度大 1 ，其他点出度等于入度。

求解欧拉路与欧拉回路一直以来是个难题，并没有很精巧的办法，基本都是暴力搜索的形式，如果搜到了满足条件的就找到了。

算法流程

只探讨求解欧拉路的算法，算法核心就是使用 DFS 栈无边回溯来求解。

整个过程：从开始节点 DFS 遍历图，每遍历一个节点就把它放入 DFS 栈中，如果当前节点存在边，就按照边去继续遍历，并标记当前边为已访问。如果当前节点不存在边，就将这个节点 pop 出去回溯。并把这个回溯的边记录下来，这条边就是欧拉通路之一。例子如下

遍历到节点 E，E 存在边，将 E 推入栈，并根据边 E->F 访问 F 节点

F 节点无边，就把 F 节点 pop 出去回溯，然后记录下回溯的边 E->F

重复以上的过程直到所有边被遍历完（所有边遍历完后会一直回溯还原整条欧拉通路）

例题

欧拉通路模板题，这里需要注意的是要判断是否存在欧拉通路，有向图判断欧拉通路要求所有点是连通的且最多只有一个点出度比入度大 1，另一个点入度比出度大 1 ，其他点出度等于入度。

这里要求输出字典序最小的欧啦路径，那就按照目标节点的字典序排序所有边，然后根据下标去访问边即可。然后使用了递归代替 DFS 栈。

剩下就是标程了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<iostream>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int ind[N],outd[N];
int n,m;
stack<int> s;
int flag[N];
vector<int> edge[N];

//判断是否存在欧拉通路
int isEular(){
    //默认起始点是 1
    int start=1;
    bool allzero = true;
    int sum1 = 0, sum2 = 0;
    for(int i=1;i<=n;i++){
        if(ind[i]!=outd[i]){
            allzero = false;
        }
        if(ind[i]-outd[i]>1){
            return -1;
        }
        if(ind[i]-outd[i]==1){
            sum1++;
        }
        if(ind[i]-outd[i]==-1){
            //如果出现了特殊情况的点就将它作为开始点
            start = i;
            sum2++;
        }
    }
    if(!(allzero||((sum1==sum2)&&sum1==1))){
        return -1;
    }
    return start;
}

void dfs(int u){
    //flag记录访问了多少条边，顺便可以访问到了哪条边的 index
    while(flag[u] < edge[u].size()){
        int tmp = flag[u];
        flag[u]++;
        //使用了递归代替栈
        dfs(edge[u][tmp]);
    }
    //没有边了，把他推到路径栈中
    s.push(u);
}

int main(){
    cin>>n>>m;
    int u,v;
    for(int i=1;i<=m;i++){
        cin>>u>>v;
        edge[u].push_back(v);
        outd[u]++;ind[v]++;
    }
    for(int i=1;i<=m;i++){
        sort(edge[i].begin(),edge[i].end())
    }
    int start = isEular();
    if(start<0){
        cout<<"No"<<endl;
    }
    else{
        dfs(start);
        while(!s.empty()){
            cout<<s.top()<<" ";
            s.pop();
        }
    }
    return 0;
}

强连通分量

基本概念

强连通分量就是对于一个图，根据可达关系对图内的节点进行聚类操作，要求分量内的任意两点相互可达，而且这个分量是最大的子集（即新加入一个其他节点就会破坏这种强连通性）。

上图中存在 4 个强连通分量

算法流程

这里介绍 Kosaraju 算法求解强连通分量。

Kosaraju 算法分为几个步骤：

  1. 把边反向，得到反向图 $G^R$
  2. 在 $G^R$ 上执行 DFS，得到顶点完成时刻顺序 $L$ （即这个顶点可达的顶点全被访问过，就加入 $L$ ）
  3. 在 $G$ 上按照 $L$ 逆序执行 DFS，得到强连通分量

例题：

强联通分量模板题，根据上面的算法内容写代码即可，没什么 skills。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N = 10005;
vector<int> g[N], rg[N];
bool vis[N];
int L[N];
int n,m,k;
void dfs1(int u){
    vis[u]=true;
    for(int i=0;i<rg[u].size();i++){
        if(!vis[rg[u][i]]){
            dfs1(rg[u][i]);
        }
    }
    L[++k]=u;
}
void dfs2(int u){
    vis[u]=false;
    for(int i=0;i<g[u].size();i++){
        if(vis[g[u][i]]){
            dfs2(g[u][i]);
        }
    }
}

void init(){
    k = 0;
    for(int i=0; i<=n; i++){
        g[i].clear();
        rg[i].clear();
    }
    memset(vis, 0, sizeof(vis));
    memset(L,0,sizeof(L));
}

int main(){
    while(cin>>n>>m&&n){
        init();
        int u,v;
        for(int i=0;i<m;i++){
            cin>>u>>v;
            g[u].push_back(v);
            rg[v].push_back(u);
        }
        for(int i=1;i<=n;i++){
            if(!vis[i])
                dfs1(i);
        }
        int cnt=0;
        for(int i=n; i>=1;i--){
            if(vis[L[i]]){
                cnt++;
                dfs2(L[i]);
            }
        }
        if(cnt==1) cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
}

最短路径算法

最短路径就是在图中，给定起点和终点，求起点到终点开销最小的路径。

存在最短路径的充要条件是最小路径不通过负环（因为负环有可能和最小路径不连通，这个时候就存在最短路径）。

对于没有负环的图，假设有 $n$ 个点，最短路径不会经过重复的顶点或者边，所以最短路径最多经过 $n$ 个点，最多经过 $n-1$条边。

Bellman-Ford 算法

基本算法

贝尔曼福特算法的核心思想就是松弛操作，松弛操作就是遍历过程中每次都尝试更新所有关联的边，假设遍历到边$(u,v)$，松弛公式如下：

$$ dist(u) = min(dist(u),dist(u)+w(u,v)) $$

大体思路很简单，遍历所有边，然后根据这个边去松弛其他所有边，整个遍历过程要迭代。

  • 如何保证贝尔曼福特算法一定结束

在最短路能够找到的情况下，从起始点开始，最多进行 $n-1$ 次迭代，因为每次迭代，都代表源点的探索多了一层（多探索到至少一个节点），最多 $n-1$ 个节点，所以最多迭代 $n-1$ 次就能找到最短路（涵盖了所有情况）

  • 贝尔曼福特算法的复杂度

由于进行 $n$ 次迭代，每次迭代都要遍历所有 $m$ 条边，所以复杂度为 $O(m*n)$

  • 如何判断达到了负环

如果发现迭代了 $n$ 次以上，就 break 掉，然后判断图中出现了负环。

标程例题

标程，细节就是由于 $max(\sum w) = 2^{31}$，这是一个很大的数，要记得开 longlong 类型防止 int 类型溢出了，且因为这个题没有负权边，所以不用考虑负环找不到的最短路的情况。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<iostream>
const int N = 10010;
const int M = 500010;
using namespace std;
int n,m,s;
long long dist[N];
struct Edge{
    int a,b,w;
}edges[M];

int bellman_ford(){
    // 初始化
    for(int i=1;i<=n;i++){
        dist[i] = (1<<31)-1;
    }
    dist[s]=0;
    for(int i=1;i<=n;i++){
        bool relaxed = false;
        for(int j=0;j<m;j++){
            int a=edges[j].a;
            int b=edges[j].b;
            int w=edges[j].w;
            if(dist[b]>dist[a]+w){
                dist[b]=dist[a]+w;
                relaxed=true;
            }
        }
        if(!relaxed) break;
    }
    //这里如果存在负环的话要记得写一个逻辑返回-1
    return dist[n];
}

int main(){
    cin>>n>>m>>s;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        edges[i]={a,b,w};
    }
    int t = bellman_ford();
    for(int i=1;i<=n;i++){
        cout<<dist[i]<<" ";
    }
    return 0;
}

SPFA 队列优化

Bellman-Ford 算法是可以进行优化的，我们看到标准的贝尔曼福特算法中是固定的 pattern，他每次迭代都会遍历所有边，但这个遍历操作实际上是没必要的，因为并不是所有边都会有机会松弛。

SPFA 优化就是根据当前松弛的结果，将下一次可能会松弛的节点对应的边加入一个队列当中，依据就是，只有在本次松弛受到影响节点（更新过距离节点），下一次才可能发生松弛。

但是 SPFA 由于不会每次都访问所有边，所以它默认不能判断是否有负环，如果要判断，要加一个 pre 数组记录路径。

同样是和上面一样的题，给一个 SPFA 优化后的代码，使用队列实现

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<vector>
#include<queue>
#include<utility>
const int N = 10010;
using namespace std;
typedef pair<int,int> PII;
int n,m,s;
long long dist[N];
vector<PII> edges[N];
bool vis = {false};

void SPFA(){
    // 初始化
    for(int i=1;i<=n;i++){
        dist[i] = (1<<31)-1;
    }
    dist[s]=0;
    queue<int> que;
    que.push(s);
    vis[s] = 1;
    while(!que.empty()){
        int u = que.front();
        que.pop();
        vis[u] = 0;
        for(int i=0;i<edges[u].size();i++){
            int v = edges[u][i].first;
            int w = edges[u][i].second;
            if(dist[v]>dist[u]+w){
                dist[v] = dist[u]+w;
                if(!vis[v]){
                    que.push(v);
                    vis[v] = true;
                }
            }
        }
    }
}

int main(){
    cin>>n>>m>>s;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        edges[a].push_back(make_pair(b,w));
    }
    SPFA();
    for(int i=1;i<=n;i++){
        cout<<dist[i]<<" ";
    }
    return 0;
}

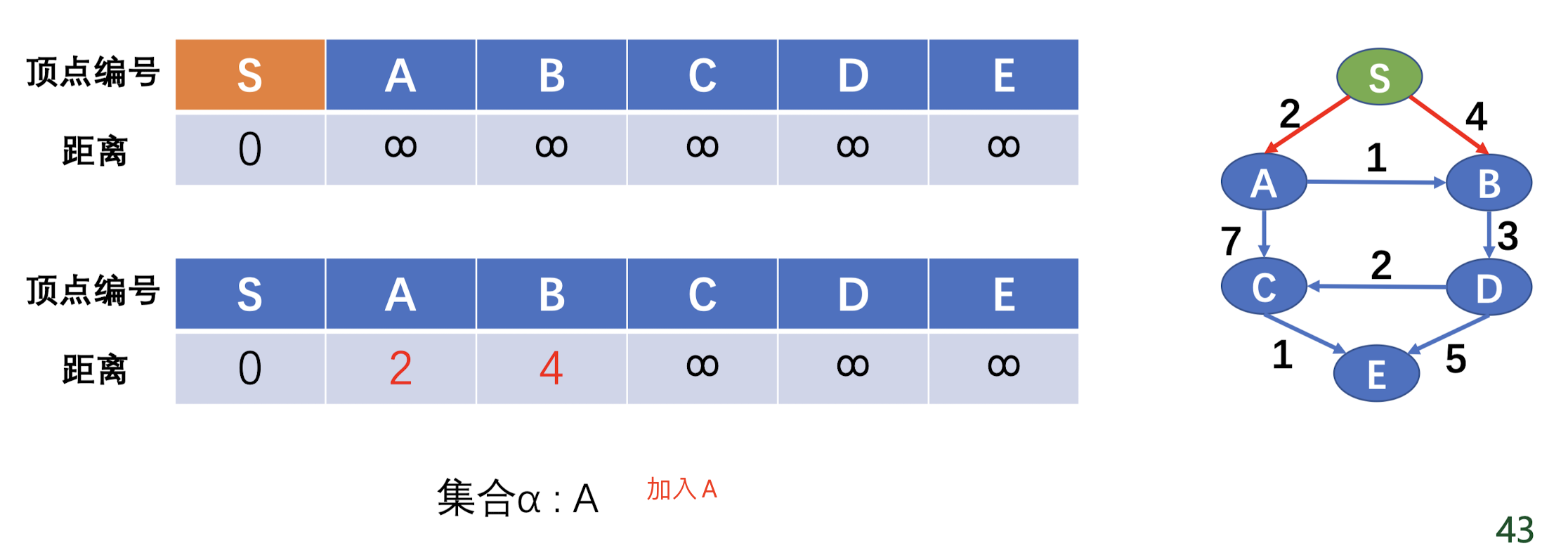
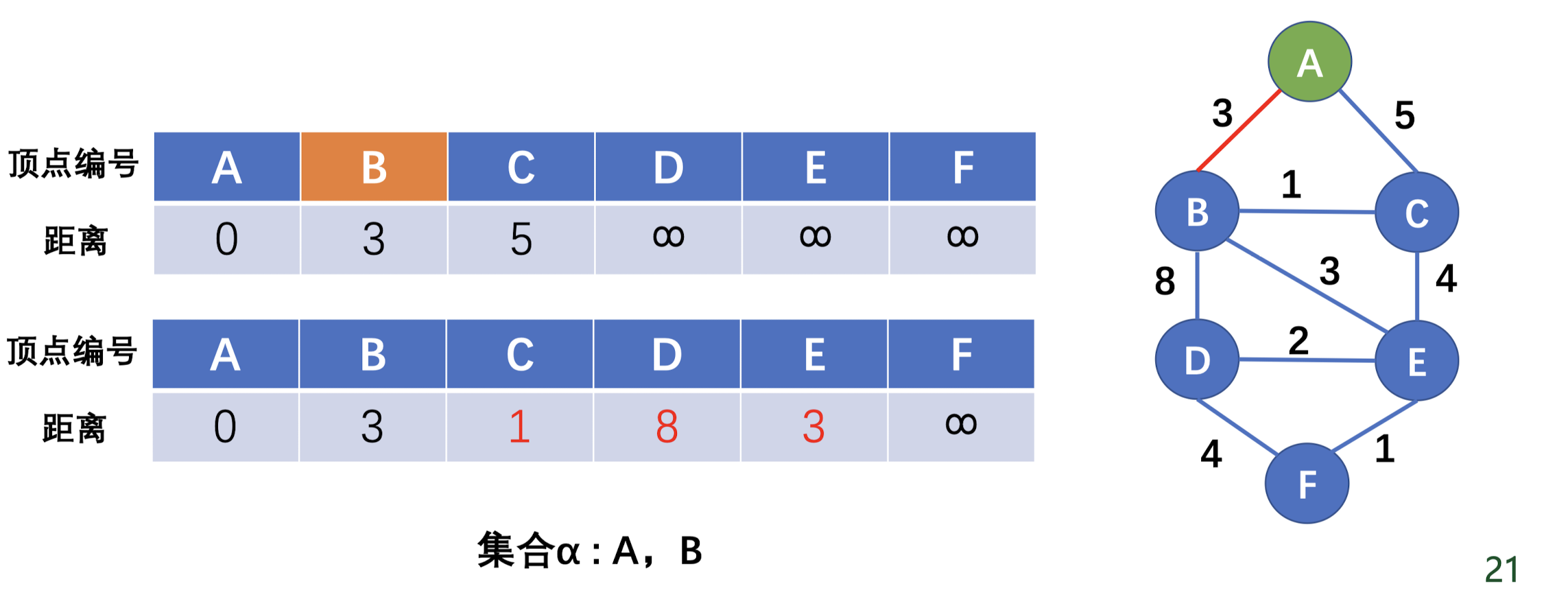
Dijkstra 算法

基本算法

Dijkstra 算法用于求无负权边的最短路径。算法的流程就是维护一个顶点集合 $\alpha$，每一轮将离起点最近的顶点加入 $\alpha$ 当中，并根据这个点的边做松弛操作。直到所有点被加入到 $\alpha$ 中。

可优化的点是，这个离起点最近的点可以使用优先队列进行优化，就可以省去排序的复杂度，复杂度为 $O(mlogn)$，优化前的复杂度为 $O(n^2 + m)$

例题

例题还是这个

这里要开一个优先队列存取节点信息（与源点的距离和这个点的编号），这里要注意的是我们使用一个 pair 去来表示节点信息，优先队列默认是对 pair 的 first 节点做排序匹配的，要记得把距离放在 first。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int N = 10010;
int n,m,s;
long long dist[N];
typedef pair<int,int> PII;
vector<PII> edges[N];
bool vis[N] = {false};

void Dijkstra(){
    // 初始化
    for(int i=1;i<=n;i++){
        dist[i] = (1<<31)-1;
    }
    dist[s]=0;
    //小根堆
    priority_queue<int,vector<int>,greater<int> heap;
    heap.push({0,s});
    while(!heap.empty()){
        auto top = heap.top();
        heap.pop();
        int u = top.second;
        int dis = top.first;
        if(vis[u])
            continue;
        vis[u] = 1;
        for(int i=0;i<edges[u].size();i++){
            int v = edges[u][i].second;
            int w = edges[u][i].first;
            if(dist[v]>dis + w){
                dist[v] = dis+w;
                heap.push({dist[v],v});
            }
        }
    }
}

int main(){
    cin>>n>>m>>s;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        edges[a].push_back(make_pair(w,b));
    }
    Dijkstra();
    for(int i=1;i<=n;i++){
        cout<<dist[i]<<" ";
    }
    return 0;
}

多源汇最短路径 - Floyd 算法

多源汇最短路径就是求所有点的最短路径，因为贝尔曼福特和Dijkstra 算法都是针对单源路径的，他们的复杂度会和边数 $m$ 有关，如果在乘上一个 $n$ 会导致复杂度很高。

Floyd 算法能够一次性出求多源汇最短路径，他的复杂度为 $O(n^3)$，算法的基本思想是开一个邻接矩阵，然后枚举每一个点为松弛过程中的中间点的情况下，再去遍历所有边：

例题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;

const int N = 110;
int n,m;
int dist[N][N];

void Floyd(){
    for(int k=1; k<=n; k++){
        for(int i=1; i<=n;i++){
            for(int j=1;j<=n;j++){
                dist[i][j] = min(dist[i][j],dist[i][k]+dist[k][j]);
            }
        }
    }
}

int main(){
    cin>>n>>m;
    memset(dist,0x3f,sizeof(dist));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j){
                dist[i][j]=0;
            }
        }
    }
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        dist[a][b]=w;
        dist[b][a]=w;
    }
    Floyd();
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<dist[i][j]<<" ";
        }
        cout<<endl;
    }
}

最小生成树算法

基本概念

生成树就是由母图派生出的一条连通路径，满足树的结构，树一般情况下是没有回路的图（只有一种情况：树可以为空，但是图不行，所以严格来说树并不包含于图）。对于一个 $n$ 阶 $m$ 条边的图，其生成树满足 $m=n-1$。

最小生成树就是有权无向连通图中边权和最小的生成树。

Prim 算法求解最小生成树

和 Dijkstra 算法类似，都是维护一个顶点集，然后从初始顶点开始遍历，每次选择边权最小的节点跳转并加入顶点集，此时的状态就是在这个节点，然后根据这个节点的边去更新距离。重复以上过程，直到没有点加入顶点集，算法结束，如果此时所有点都在集合内，则说明找到了最小生成树。

Prim 算法的复杂度为 $O(n^2+m)$

例题：

标程题，注意他这里要输出最小生成树的边权和，所以迭代过程中直接加上权值就好。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<iostream>
#include<cstring>
#include<utility>
#include<vector>
using namespace std;
const int N = 510;
int n,m;
int dist[N];
typedef pair<int,int> PII;
vector<PII> edges[N];
bool vis[N]={false};

int Prim(){
    memset(vis,false,sizeof(vis));
    memset(dist,127,sizeof(dist));
    dist[1]=0;
    int res=0,tot=0;
    while(true){
        int flag=-1;
        // 找最小点
        for(int i=1;i<=n;i++){
            if(!vis[i]&&dist[i]<1<<30){
                if(flag==1 || dist[i]<dist[flag])
                    flag = i;
            }
        }
        if(flag==-1){
            break;
        }
        tot++;
        res+=dist[flag];
        vis[flag]=true;
        for(int i=0;i<edges[flag].size();i++){
            int v = edges[flag][i].first;
            int w = edges[flag][i].second;
            dist[v] = min(dist[v],w);
        }
    }
    if(tot!=n){
        return -1;
    }
    return res;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        //注意是无向图
        edges[a].push_back({b,w});
        edges[b].push_back({a,w});
    }
    int res = Prim();
    if(res>0){
        cout<<res<<endl;
    }
    else{
        cout<<"orz"<<endl;
    }
    return 0;
}

这里的找最小点部分，可以使用优先队列去找，会快一些，但其实没必要，因为接下来还有一个 Kruskal 算法，他能很好的代替 Prim 算法找到最小生成树。

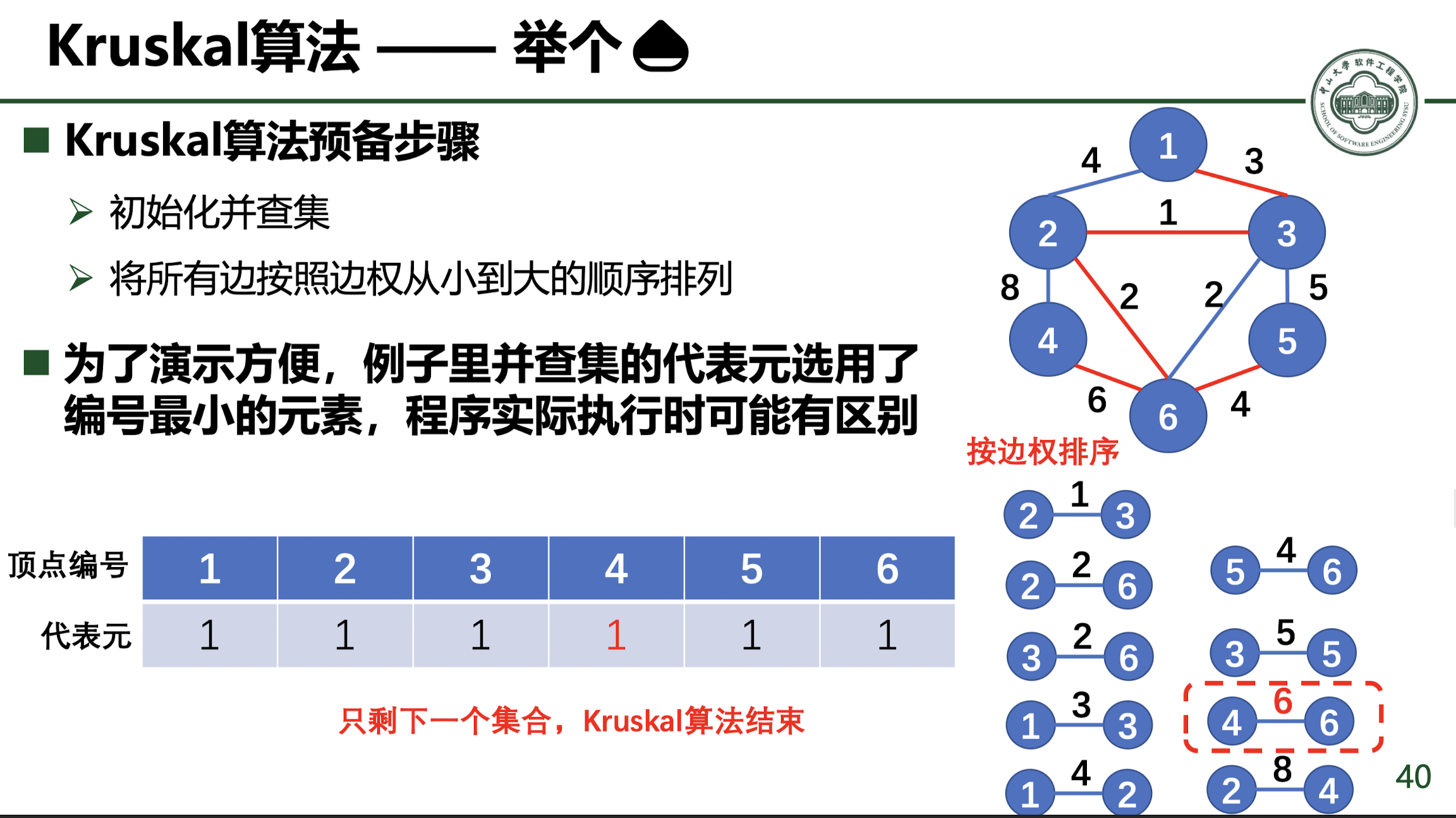
Kruskal 算法求最小生成树

Kruskal 算法与 Prim 算法不同，他是按照边进行遍历的，一条条添加边来构成最小生成树，为了避免加入边 $(u,v)$ 的时候构成环，使用并查集来检查 $u$ 和 $v$ 是否已经加入了最小生成树中，如果已经加入了，再加这条边就会构成环，所以就不能加入。

如果需要记录路径，就要开一个边数组，记录所有生效的边。

到最后只剩下一个集合，算法结束。

如何判断是否存在最小生成树呢（是否连通），可以记录加入边的个数，如果循环结束后加入边的个数小于 $n-1$，则说明不构成图生成树的条件，图不连通。

Kruskal 的复杂度为 $O(mlogn)$，比 Prim 算法高效很多。

例题，还是一样

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 5010;
const int M = 200010;
int n,m;
int p[N];
struct Edge{
    int a,b,w;
    bool operator < (const Edge &W)const{
        return w<W.w;
    }
}edges[M];

void init(){
    for(int i=0;i<=n;i++){
        p[i]=i;
    }
}

int find(int x){
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}

int Kruskal(){
    //排序所有边
    sort(edges,edges+m);
    init();
    int res=0,cnt=0;
    for(int i=0;i<=m;i++){
        int a=edges[i].a;
        int b=edges[i].b;
        int w=edges[i].w;
        a=find(a); b=find(b)
        if(a!=b){
            p[a]=b;
            res+=w;
            cnt++;
        }
    }
    if(cnt<n-1) return -1;
    return res;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b,w;
        cin>>a>>b>>w;
        edges[i] = {a,b,w};
    }
    int res = Kruskal();
    if(res>0){
        cout<<res<<endl;
    }
    else{
        cout<<"orz"<<endl;
    }
    return 0;
}

二分图算法

基本概念

二分图又称为二部图和偶图，是一个无向图，可以根据顶点之间的交集把顶点分为两个部分，每个部分内的顶点互不相交，至于另外那个部分的顶点相交。

完全二分图就是集合 $X$ 和集合 $Y$ 中每对顶点有且只有一条边的二分图，记为 $K_{n-m}$，$n$ 为 $X$ 中顶点的个数，$m$ 为 $Y$ 中顶点的个数。

染色法判定二分图

染色法就是一个边遍历边染色的二分图判定法，首先选取一个还没有被染色的节点，从他开始做 dfs 或者 bfs 遍历，先给他分配一个初始颜色，当遍历到边 $u$->$v$ 时，如果 $v$ 未被染色，就将 $v$ 染色成 $u$ 对立的那个颜色；如果 $v$ 已经被染色，则说明出现冲突，不存在二分图。

例题

这里需要开一个数组去记录颜色，同时要记录三种状态：未染色，颜色 A，颜色 B。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int N = 200010;
vector<int> edges[N];
int n,m,color[N];// 0表示未染色，1,2 表示不同颜色

bool dfs(int x){
    for(auto y:edges[x]){
        if(!color[y]){
            color[y] = 3-color[x];
            if(!dfs(y)) return false;
        }
        else{
            if(color[y]==color[x])
                return false;
        }
    }
    return true;
}

bool check(){
    memset(color,0,sizeof(color));
    for(int i=1;i<=n;i++){
        if(!color[i]){
            color[i]=1;
            if(!dfs(i)) return false;
        }
    }
    return true;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        //注意是无向图
        edges[a].push_back(b);
        edges[b].push_back(a);
    }
    if(check()){
        cout<<"Yes"<<endl;
    }
    else{
        cout<<"No"<<endl;
    }
}

匈牙利算法解决二分图匹配问题

把二分图 $G=<V, E>$ 的顶点集$V$拆分成 $V1$ 和$V2$，选取一些边 $E^′ ⊆ E$，如果 $E^′$ 中任意两条边都没有相同的顶点，则称 $E^′$ 为G的匹配。

而二分图的最大匹配就是边数最多的边集 $E^′$。

如下图中的最大匹配就是红边的集合，大小为 4。

匈牙利算法就是解决二分图最大匹配问题的，他的核心思路就是遍历所有节点的边，然后匹配前看对方节点是否已经被匹配，如果没有被匹配就直接和它匹配，如果被匹配了，就看这个节点匹配的那个节点能不能换一个节点匹配，如果可以，就更换然后匹配，如果不行，就遍历下一个节点。

我们老师给的浅显易懂的图示

例题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int N = 1010;
vector<int> edges[N];
int n,m,e;
int aim[N];
int vis[N];
bool find(int x){
    for(auto y:edges[x]){
        // 如果在这一轮中没被问
        if(!vis[y]){
            vis[y]=true;
            // 递归去询问
            if(aim[y]==0||find(aim[y])){
                aim[y]=x;
                return true;
            }
        }
    }
    return false;
}

int match(){
    int ans=0;
    memset(aim,0,sizeof(aim));
    for(int i=1;i<=n;i++){
        //记得初始化
        memset(vis,false,sizeof(vis));
        if(find(i)){
            ans++;
        }
    }
    return ans;
}

int main(){
    cin>>n>>m>>e;
    for(int i=1;i<=e;i++){
        int a,b;
        cin>>a>>b;
        edges[a].push_back(b);
    }
    cout<<match()<<endl;
    return 0;
}

之后有空会复习，补充网络流的内容。