【数字图像处理】 SRCNN 图像超分辨率
使用深度卷积网络实现图像超分辨率
简介
单图像超分辨率(SR)是从一张模糊的低分辨率图像创建出一张清晰的高分辨率图像的技术。这个过程在计算机视觉中既常见又复杂,因为低分辨率图像中的每个像素可以对应多种高分辨率版本。为解决这个问题,研究者们通常使用已知的信息来指导图像的高分辨率重建。
最新的一种方法是使用深度学习,特别是一种叫做超分辨率卷积神经网络(SRCNN)的技术。与传统方法不同,SRCNN不是通过学习和重复使用图像块的模式来提高分辨率,而是通过一个深度网络直接学习从低分辨率到高分辨率图像的转换。这个网络减少了需要的预处理和后处理步骤,并且能够在保持简单结构的同时,提供优于传统方法的图像质量。
SRCNN的另一个优势是它可以快速运行,即使是在普通的计算机CPU上也能实现实时处理。此外,随着训练数据集的扩大和模型结构的深化,SRCNN的性能还有进一步提升的潜力。它甚至可以同时处理彩色图像中的三个颜色通道,从而进一步提高图像的超分辨率效果。简而言之,SRCNN是一个更高效、更强大的图像超分辨率工具。
这篇论文的主要贡献有三个方面:
- 提出了一个全卷积神经网络用于图像超分辨率。这个网络直接学习从低分辨率到高分辨率图像的端到端映射关系,除了优化过程之外几乎不需要任何预处理或后处理。
- 建立了基于深度学习的超分辨率方法与传统基于稀疏编码的超分辨率方法之间的关系。这一关系为网络结构的设计提供了指导。
- 展示了深度学习在经典的计算机视觉问题——图像超分辨率中的应用价值,能够实现良好的质量和速度。
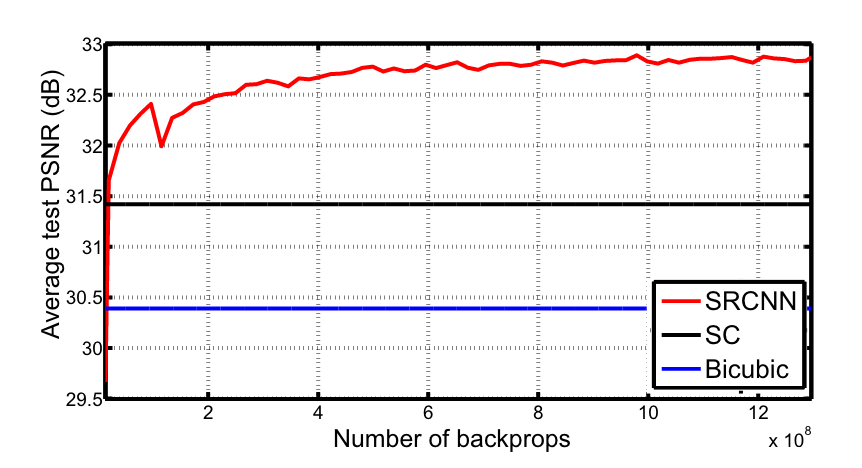
图1展示了SRCNN如何在经过少量训练迭代后就超过了双三次插值(bicubic)这一基准方法,并在中等程度的训练后胜过了基于稀疏编码的方法(SC)
这四张图显示了不同超分辨率方法处理同一图像后的结果,其中每张图下方的dB值表示峰值信噪比(PSNR)的数值。PSNR是一种评估图像质量的指标,通常用于衡量原始图像与重建或压缩后图像之间的相似度。数值越高,表示误差越小,图像质量越好。这些dB值展示了每种方法重建的图像质量与原始图像的接近程度:
- 原始图像/PSNR:是原始高分辨率图像的参考标准,不显示dB值。
- 双三次插值/Bicubic:24.04 dB,表示使用双三次插值方法后的图像质量评分。
- 基于稀疏编码的方法/SC:25.58 dB,表示使用稀疏编码方法后的图像质量评分。
- 超分辨率卷积神经网络/SRCNN:27.95 dB,表示使用SRCNN方法后的图像质量评分,是这些方法中最高的,表明SRCNN提供了最接近原始图像的重建效果。
相关知识介绍
超分辨率算法的分类介绍:
根据图像的先验特征(image piror),我们对单图像使用的超分辨率算法(single image super-solution algorithm, SISR algorithm)可以分为四类,预测模型(prediction models)、基于边缘方法(method based methods)、基于块(基于实例)方法(patch based (or example based) methods)、图像统计方法(image statistical methods)。
-预测模型(prediciton model): 通过利用预定义的某种数学模型而不借助输入的图像数据训练去估计对应的高分辨率图像,从而完成超分辨率任务。例如,各类插值方法等。
-基于边缘方法(edge based model): 基于图像边缘(edge)这一先验特征的学习而构造的算法。如基于梯度剖面(gradient profile)的学习方法(learning method)。
-基于块(基于实例)方法(patch based (or example based) methods):通过LR/HR图像间子块(patch)的关系,利用加权平均[8,1]、核回归[6]、支持向量回归[7]等方法学习映射函数后完成超分
辨率任务的算法。
-图像统计方法(image statistical methods):基于多种图像先验特征而构造的算法。
基于块(基于实例)方法分类介绍:
其中基于块(基于实例)方法可以分为两类,基于示例内部联系的方法(internal example based methods)和基于示例外部联系(external example based methods)的方法。
基于示例内部联系的方法利用图像内部的相似性,从输入图像中直接生成样本子块。最初是在Glasner的工作[5]中提出的,后续还提出了一些改进的变体[3]、[11]以加快处理速度。
基于示例外部联系的方法[1]、[2]则学习来自外部数据集的低/高分辨率子块之间的映射关系。这些研究探讨了如何学习紧凑的字典或流形空间来关联低/高分辨率子块,以及如何在这些空间中进行表示。在Freeman等人的先驱工作中[4],字典直接呈现为低/高分辨率子块对,然后在低分辨率空间中找到输入子块的最近邻(NN),并利用其对应的高分辨率子块进行重建。Chang等人[2]则引入了流形嵌入技术作为NN策略的替代方法。在杨等人的工作[12]、[13]中,上述NN对应关系演变成更复杂的稀疏编码公式。其他映射函数,如核回归、简单函数、随机森林和锚定邻域回归等等被提出以进一步提高映射的准确性和速度。基于稀疏编码的方法及其若干改进[9]、[10]如今处于最先进的超分辨率方法之列。在这些方法中,子块是优化的重点;子块提取和聚合步骤被视为前/后处理并分别处理。
用于超分辨率的卷积神经网络
方程
考虑一张单一的低分辨率图像,我们首先使用双三次插值将其放大到所需的尺寸,这是我们唯一进行的预处理步骤。让我们将插值后的图像表示为$ Y $。我们的目标是从$ Y $中恢复出一张图像 $ F(Y) $,尽可能地与真实的高分辨率图像 $ X $ 相似。为了方便说明,我们仍然将$ Y $称为“低分辨率”图像,尽管它与X具有相同的尺寸。我们希望学习一个映射 $ F $,它概念上包含三个操作:
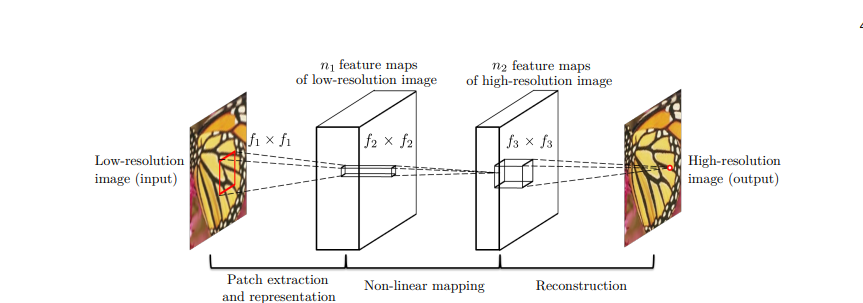
-补丁提取与表示:该操作从低分辨率图像$ Y $中提取(重叠的)补丁,并将每个补丁表示为高维向量。这些向量构成一组特征图,其数量等于向量的维度。
-非线性映射:该操作将每个高维向量非线性映射到另一个高维向量。每个映射后的向量在概念上是高分辨率补丁的表示。这些向量构成另一组特征图。
-重构:该操作聚合上述高分辨率补丁的表示,生成最终的高分辨率图像。这个图像预期与真实的高分辨率图像 $ X $ 相似。
我们将展示所有这些操作构成了一个卷积神经网络。网络的概览如图2所示。接下来,我们j将说明每个操作的形式化定义。
步骤1:补丁提取与表示
用一组预先训练的基作为滤波器,对图像进行卷积,将此步操作记为$ F_1(Y) $。
具体来说:
$$
F_1(Y) = \max(0, W1 * Y + B1)
$$
其中,$ W_1 $ 和 $ B_1 $ 分别代表滤波器和偏置,符号 ‘$ \ast $’ 表示卷积操作。这里的 $ W_1 $ 对应于支持尺寸为 $ c \times f_1 \times f_1 $ 的 $ n_1 $ 个滤波器,其中 $ c $ 是输入图像中的通道数,$ f_1 $ 是滤波器的空间尺寸。直观来说,$ W_1 $ 对图像应用了 $ n_1 $ 次卷积,每次卷积都有尺寸为 $ c \times f_1 \times f_1 $ 的核。输出由 $ n_1 $ 个特征图组成,$B_1$ 是一个 $ n_1 $ 维向量,其每个元素与一个滤波器相关联。最后,他们对滤波器的响应应用了ReLU激活函数。
步骤2:非线性映射
这段描述了非线性映射的过程。第一层从每个补丁中提取一个 $ n_1$ 维的特征。在第二个操作中,将这些 $n_1$ 维向量映射为一个 $ n_2 $ 维向量。这相当于应用了具有平凡空间支持 1×1 的 $ n_2 $个滤波器。这种解释仅适用于 1×1 的滤波器。但是可以很容易地推广到更大的滤波器,比如 3×3 或 5×5。在这种情况下,非线性映射不是作用在输入图像的一个补丁上;相反,它是作用在特征图的一个 3×3 或 5×5 的“补丁”上。第二层的操作是:
$$
F_2(Y) = \max(0, W_2 * F_1(Y) + B_2)
$$
这里的 $ W_2 $ 包含尺寸为 $ n_1 \times f_2 \times f_2 $ 的 $ n_2 $ 个滤波器,$ B_2 $ 是 $ n_2 $ 维的。每个输出的 $ n_2 $ 维向量在概念上是一个高分辨率补丁的表示,将用于重建。
可以添加更多的卷积层来增加非线性。但这可能会增加模型的复杂性(一个层有 $n_2 \times f_2 \times f_2 \times n_2 $个参数)。
步骤3:重构
这一部分描述了重建的过程。传统方法中,预测出的重叠高分辨率补丁通常被平均以生成最终的完整图像。这种平均可以被视为一组特征图上的预定义滤波器(每个位置是高分辨率补丁的“展平”向量形式)。受此启发,他们定义了一个卷积层来生成最终的高分辨率图像:
$$
F(Y) = W_3 * F_2(Y) + B_3
$$
这里的 $ W_3 $ 对应尺寸为 $ n_2 \times f_3 \times f3 $ 的 c 个滤波器,$ B_3 $ 是一个 $c$ 维的向量。
如果高分辨率补丁的表示是在图像域中(即,可以简单地重塑每个表示以形成补丁),我们期望这些滤波器像平均滤波器一样起作用;如果高分辨率补丁的表示在其他域中(例如,某些基的系数),我们期望 $W_3$ 的行为类似于先将系数投影到图像域,然后再进行平均。在任何情况下,$W_3$ 都是一组线性滤波器。
以上为卷积神经网络图示
和稀疏编码的关系
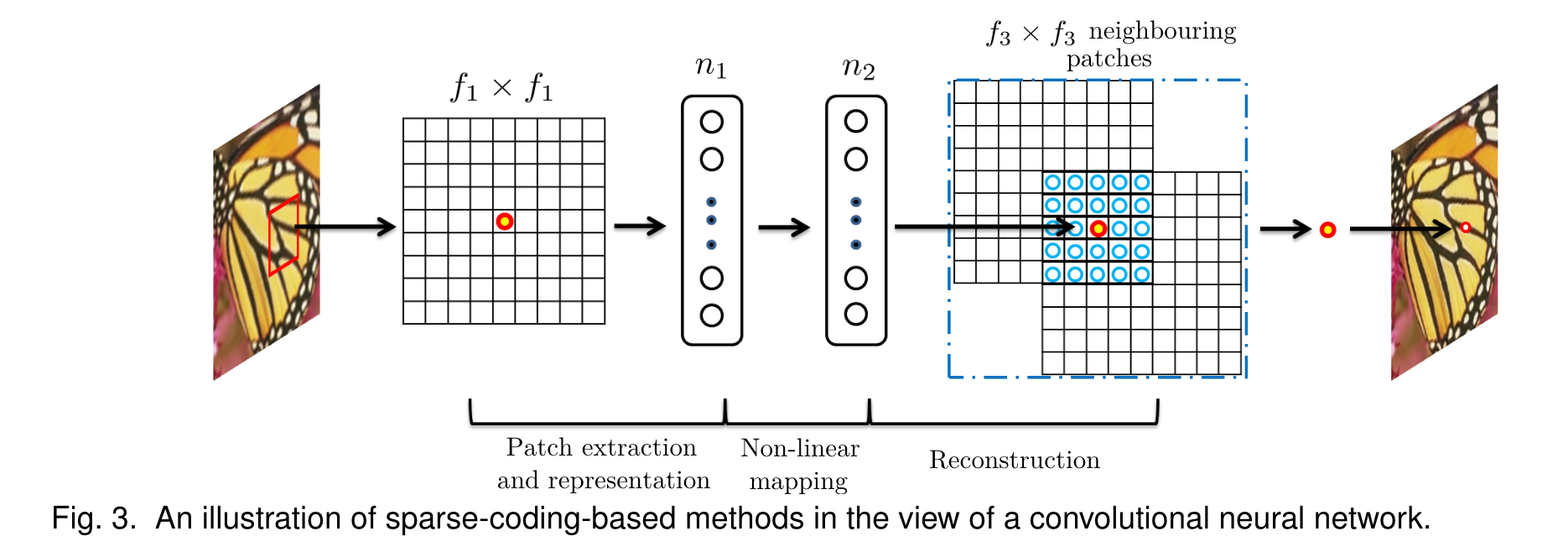
基于稀疏编码的超分辨率( SR) 方法可以看作是一个卷积神经网络。下图进行了详细说明
- 提取和表示补丁(Patch Extraction and Representation):从输入图像中提取一个 $f_1 \times f_1$ 的低分辨率小方块。然后,稀疏编码解算器首先将方块投影到一个低分辨率字典上。这个“字典”是由很多标准化的小图块组成的,用来帮助我们理解和重构图片的内容。如果字典的大小是 $n_1$,这相当于在输入图像上应用 $n_1$ 个线性滤波器($f_1 \times f_1$)。投影这个补丁到字典上,就好比是在原来的模糊图片上应用了 $n_1$ 个不同的滤镜,每个滤镜对应字典中的一个小块。每个滤镜都会尝试从你的补丁中找出最接近它的那部分内容。
- 非线性映射(Non-linear mapping):稀疏编码解算器随后迭代处理这$n_1$个系数。这个解算器的输出是$n_2$个系数,通常情况下,$n_2 = n_1$。这些$n_2$个系数代表了高分辨率补丁的表示。稀疏编码解算器在这里相当于一个特殊的“翻译器”,它把输入的图像块(在第一个步骤中得到的)转换为一组新的数值(称为系数),这些新数值代表了图像补丁在更高分辨率版本中的信息。这种转换是非线性的,意味着它能够捕捉输入数据之间复杂的关系,而不是简单的直线关系。参见图3中间部分。然而,这个稀疏编码解算器并不是一个简单的一步到位的过程(不是前馈的),它是通过多次迭代计算来逐渐接近最终结果的,这意味着它会不断地调整它的输出,直到找到最合适的高分辨率表示。相反,文中提到的非线性操作器是前馈的,意味着它可以一步到位地完成计算,不需要迭代,这使得过程更快、更高效。
- 然后将上述 $n_2$ 个系数(稀疏编码后)投影到另一个(高分辨率)字典上以生成高分辨率补丁。然后对重叠的高分辨率补丁进行平均。在图像重建的最后阶段,我们使用先前得到的 $n_2$个系数(这些系数代表了我们想要重建的高分辨率图像的特征)作为输入,对它们进行一种特殊的操作,称为线性卷积。线性卷积是图像处理中常用的一种技术,它通过一系列的滤波器来改变图像的特征,以此来重建或增强图像的质量。
综上,基于稀疏编码的超分辨率方法可以看作是一种特殊的卷积神经网络,它包括了不同的非线性映射过程。但与传统的稀疏编码方法不同,作者提出的卷积神经网络将所有步骤(如字典创建、非线性映射、均值减法和平均化)集成到了一个待优化的系统中。这种方法实现了从头到尾的映射优化。
这样的类比还帮助我们在设计网络时设定超参数。比如,我们可以将网络最后一层的过滤器尺寸设置得比第一层小,这样可以让网络更加关注高分辨率图像的中心部分。同时,我们也可以减少某些层的神经元数量,因为我们期望网络表示更加稀疏。总体来说,这样的设置让重建的高分辨率像素能利用到比传统方法更多的像素的信息,也是该卷积神经网络能够提供更好性能的原因之一。
训练过程
为了学习端到端的映射函数$F$,我们需要估计网络参数$\Theta$,包括各层的权重$W_1, W_2, W_3$和偏置$B_1, B_2, B_3$。我们通过最小化重建图像$F(Y; \Theta)$和高分辨率真实图像$X$之间的差异来实现这一点。给定一组高分辨率图像${X_i}$及其相应的低分辨率图像${Y_i}$,我们使用均方误差(MSE)作为损失函数来评估这个差异:
$$
L(\Theta) = \frac{1}{n} \sum_{i=1}^{n} ||F(Y_i; \Theta) − X_i||^2,
$$
这里$n$是训练样本的数量。使用MSE有助于获得高的峰值信噪比(PSNR),这是评价图像恢复质量的一种常用指标。虽然我们的模型训练时倾向于高PSNR,但在使用其他指标,如SSIM和MSSIM评估时,仍表现良好。通过随机梯度下降和标准的反向传播来最小化损失。权重矩阵更新如下:
$$
\Delta_{i+1} = 0.9 \cdot \Delta_i − \eta \cdot \left(\frac{\partial L}{\partial W_i}\right),
$$
$$
W_{i+1} = W_i + \Delta_{i+1},
$$
其中$i$是层和迭代的索引,$\eta$是学习率。每层的滤波器权重从一个均值为0,标准差为0.001的高斯分布中随机初始化(偏置为0)。前两层的学习率为$10^{-4}$,最后一层为$10^{-5}$。我们发现最后一层较小的学习率对网络收敛很重要。
论文引用
[1] Bevilacqua, M., Roumy, A., Guillemot, C., Morel, M.L.A.: Low-complexity single-image super-resolution based on nonnegative
neighbor embedding. In: British Machine Vision Conference
(2012)
[2] Chang, H., Yeung, D.Y., Xiong, Y.: Super-resolution through neighbor embedding. In: IEEE Conference on Computer Vision and
Pattern Recognition (2004)
[3] Freedman, G., Fattal, R.: Image and video upscaling from local
self-examples. ACM Transactions on Graphics 30(2), 12 (2011)
[4] Freeman, W.T., Jones, T.R., Pasztor, E.C.: Example-based super-resolution. Computer Graphics and Applications 22(2), 56–65
(2002)
[5] Glasner, D., Bagon, S., Irani, M.: Super-resolution from a single
image. In: IEEE International Conference on Computer Vision. pp.
349–356 (2009)
[6] He, K., Sun, J.: Convolutional neural networks at constrained time
cost. arXiv preprint arXiv:1412.1710 (2014)
[7] Jia, K., Wang, X., Tang, X.: Image transformation based on learning
dictionaries across image spaces. IEEE Transactions on Pattern
Analysis and Machine Intelligence 35(2), 367–380 (2013)
[8] Mamalet, F., Garcia, C.: Simplifying convnets for fast learning.
In: International Conference on Artificial Neural Networks, pp.
58–65. Springer (2012)
[9] Timofte, R., De Smet, V., Van Gool, L.: Anchored neighborhood
regression for fast example-based super-resolution. In: IEEE International Conference on Computer Vision. pp. 1920–1927 (2013)
[10] Timofte, R., De Smet, V., Van Gool, L.: A+: Adjusted anchored
neighborhood regression for fast super-resolution. In: IEEE Asian
Conference on Computer Vision (2014)
[11] Yang, C.Y., Huang, J.B., Yang, M.H.: Exploiting self-similarities
for single frame super-resolution. In: IEEE Asian Conference on
Computer Vision, pp. 497–510 (2010)
[12] Yang, J., Wright, J., Huang, T., Ma, Y.: Image super-resolution as
sparse representation of raw image patches. In: IEEE Conference
on Computer Vision and Pattern Recognition. pp. 1–8 (2008)
[13] Yang, J., Wright, J., Huang, T.S., Ma, Y.: Image super-resolution
via sparse representation. IEEE Transactions on Image Processing
19(11), 2861–2873 (2010)