【算法】动态规划

动态规划是一个递推的问题解法，每一步递推都会获得当前情况下的最优解，与贪心不同，会根据当前情况去更改策略，要使用动态规划必须满足一下几个性质：

  • 最优子结构：大问题的最优解可以由小问题的最优解推出
  • 重叠子问题：要求子问题很小，而且在求解当前子问题的时候不会产生新的子问题
  • 无后效性：当前的最优解不会因为后面的求解而改变。

0-1 背包问题

方法

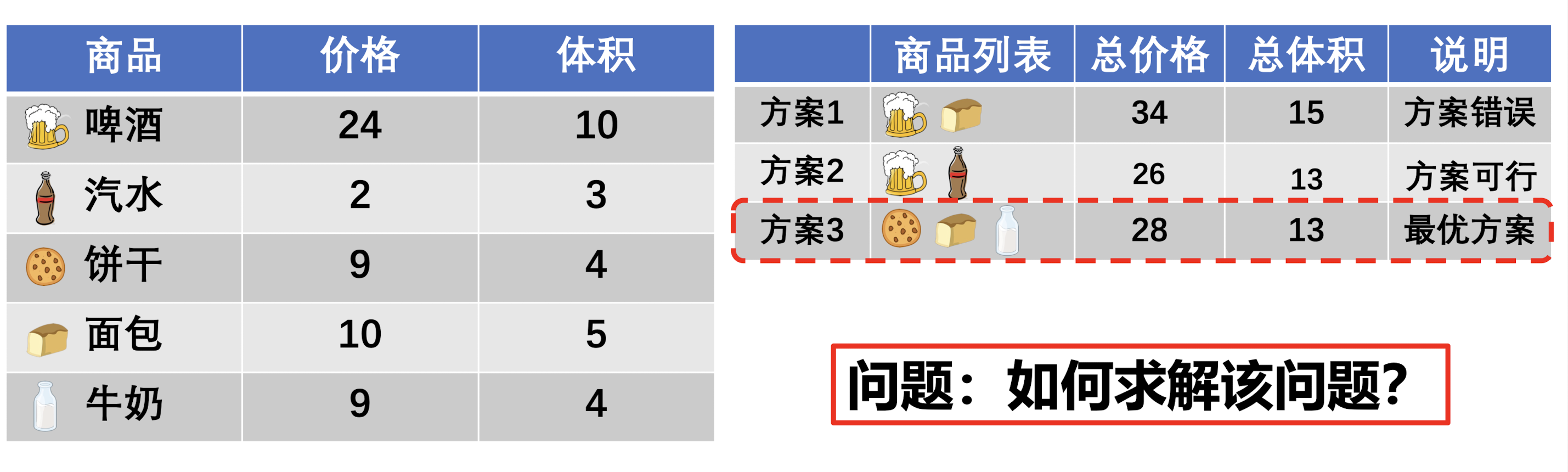
0-1 背包问题是个很经典的动态规划问题，对于下面这个问题：

上述问题可以证明贪心策略是不可行的（通过性价比去选取会忽略能够最大化利用背包空间的情况），使用动态规划的核心就是根据递推公式来维护一个动态规划表。

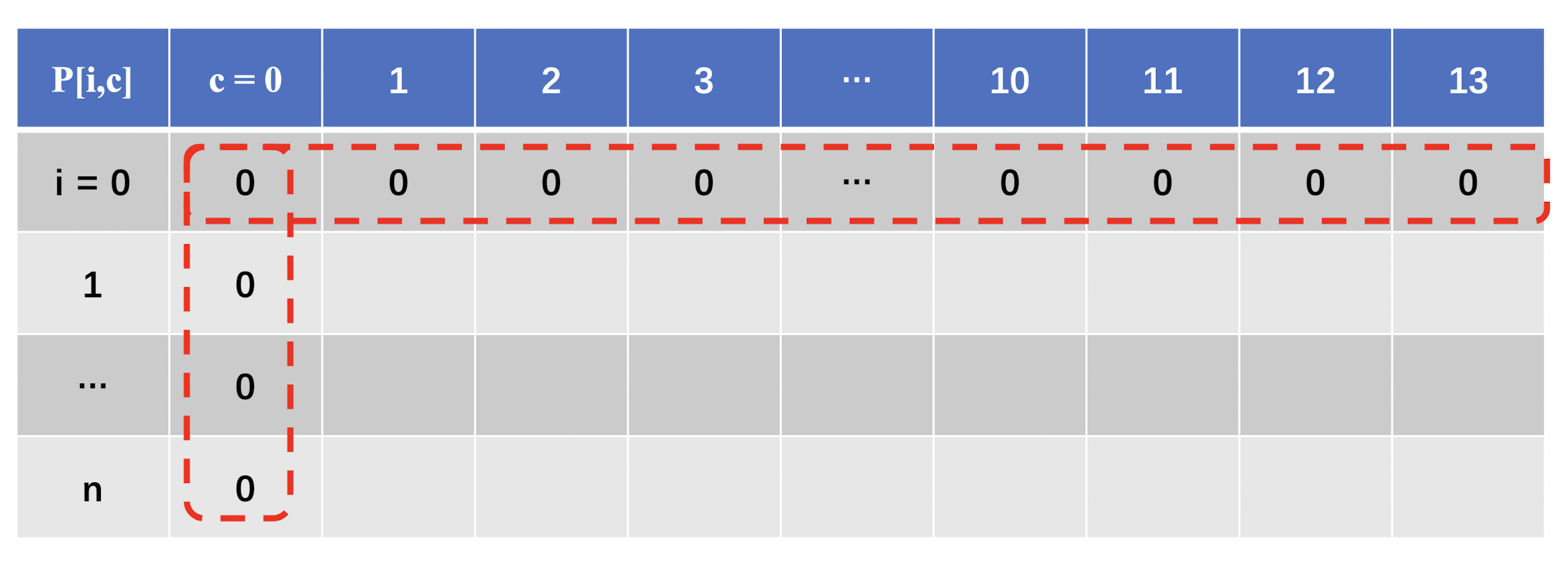
对于 0-1 背包问题，通常会选取背包容量作为纵坐标，选取物品个数作为横坐标，即 $P(i,c)$ 标识在容量为 $c$ 时，前 $i$ 个物品的最大价值，然后进行初始化，没有商品时 $P(0,c) = 0$，没选择商品时$P(i,0) = 0$：

我们从选择物品开始逐行遍历，当面对下一个物品时，无非只有两种选择：

  1. 选取这个物品，然后加上占用背包容量和价值
  2. 不选取这个物品

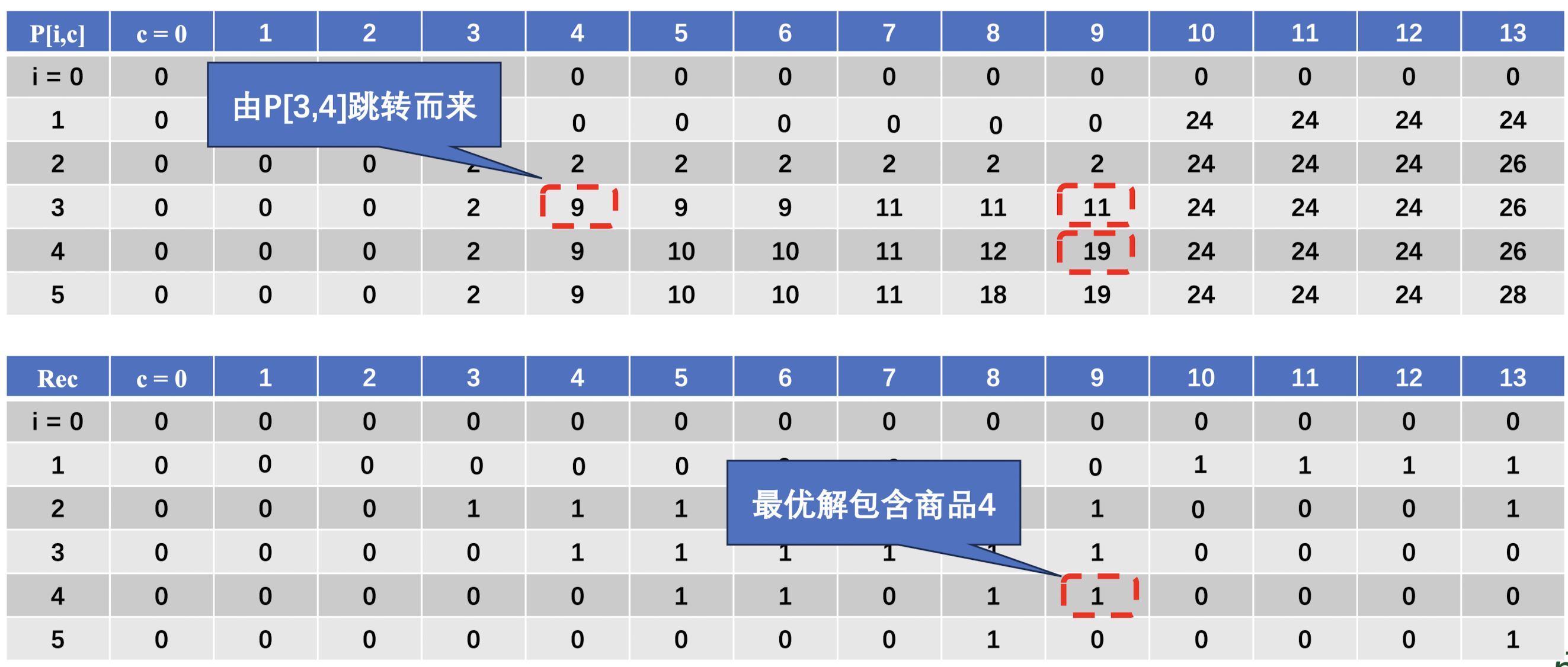
即只可能出现在当前点的左上方或者正上方，以递推方程的形式就可以表示为：

$$ P(i,c) = max(P(i-1,c-v_i)+p_i,P(i-1,c)) $$

在递推过程中，如果要追踪加入背包的商品，就要记录决策的过程，构造一个数组 $Rec[i,c]$，如果在决策过程中加入了这个商品，就令$Rec[i,c]=1$，反之等于 0

在记录过后，可以通过回溯的方式，去还原加入背包的商品，回溯过程可以是这样的，对比$P(i,c)$ 和 $P(i-1,c)$，如果不相同就说明 $P(i,c)$ 是从 $P(i-1,c-v_i)$ 跳转过来的，就直接看 $Rec[i-1,c-v_i]$ 是否为 1，如果为 1 就说明加入了编号为 $i-1$ 的商品，反之则没有。

如果 $P(i,c) = P(i-1,c)$，就看 $Rec[i-1,c]$，如果等于 1 就说明加入了编号为 $i-1$ 的商品，反之则没有

例题

经典的 0-1 背包模板题，直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
using namespace std;
int dp[110][1010];
int c[110];
int p[110];
int main(){
    int t,m;
    cin>>t>>m;
    for(int i=1;i<=m;i++){
        cin>>c[i]>>p[i];
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=t;j++){
            if(j>=c[i]){
                dp[i][j] = max(dp[i-1][j-c[i]]+ p[i],dp[i-1][j]);
            }
            else{
                dp = dp[i-1][j];
            }
        }
    }
    cout<<dp[M][T]<<endl;
    return 0;
}

动态规划解决带权区间调度问题

例题：

这道题需要构造一个结构体，结构体用于存储挤奶的开始时间，结束时间，以及收益，然后以 $DP[i]$ 作为选择当前区间的最大收益，递推思路为选择或者不选择这个区间，如果选择了当前这个区间，就要找到这个区间开始前最后结束的区间，然后加上这个区间的权重，如果不选这个区间，就跟上前一个区间的最大收益，递推方程如下：

$$DP[i] = max((DP[p[i]]+w_i),DP[i-1])$$

其中 $p[i]$ 为 $i$ 区间开始前最后结束的区间

代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<iostream>
#include<algorithm>
using namespace std;
int dp[1050];
int p[1050];
struct node{
    int start;
    int end;
    int value;
}n[1050];

bool cmp(node a,node b){
    return a.end < b.end;
}

int main(){
    int n,m,r;
    cin>>n>>m>>r;
    for(int i=1;i<=m;i++){
        cin>>n[i].start>>n[i].end>>n[i].value;
        n[i].end += r; //记得加上休息时间
    }
    sort(n+1,n+m+1,cmp);
    // 获取 p
    for(int i=m;i>=1;i--){
        for(int j=i-1;j>=1;j--){
            if(n[j].end<n[i].start){
                p[i]=j;
                break;
            }
        }
    }
    for(int i=1;i<=m;i++){
        dp[i] = max(dp[p[i]]+n[i].value,dp[i-1]);
    }
    cout<<dp[m]<<endl;
    return 0;
}

动态规划解最大子数组和

直接来看例题

因为这道题要求有序，所以不能以 0-1 背包的思路去求解。尝试去寻找规律，一般对于子数组和的问题来说，枚举起点和终点是通解（从起点或者从终点开始递推，递推可以从前往后也可以从后往前），可以尝试从起点终点序列和的性质入手。

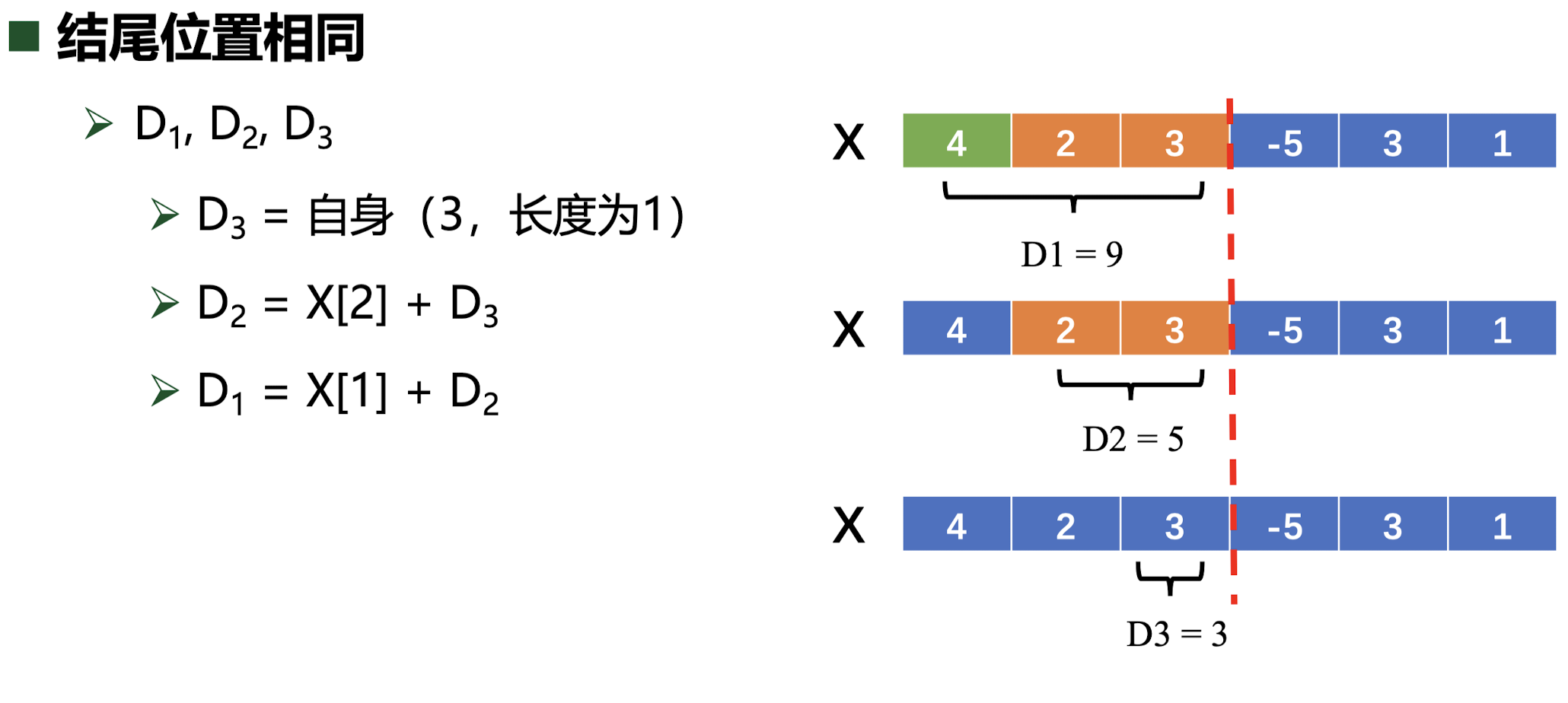
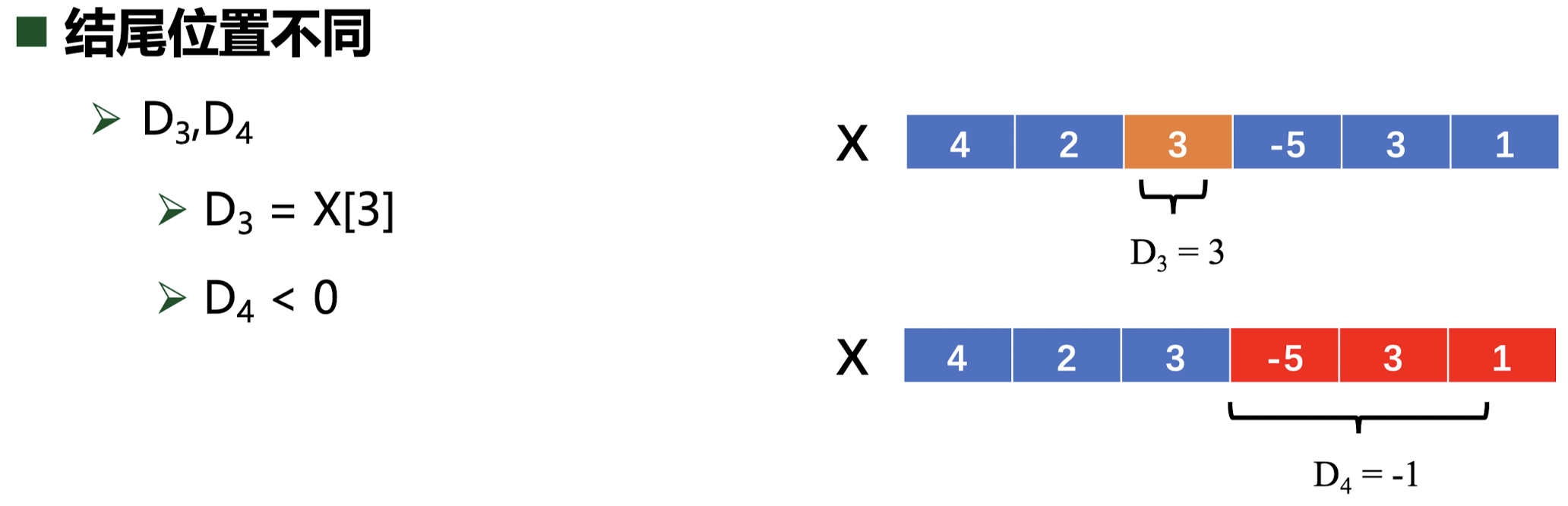
不难发现，如果我们从后往前去枚举起点，其实是有规律性的

在这里如果在自己作为起点时，前面那个点的的最大子数组和大于 0 的话，就可以直接加上，如果不大于 0 的话，就不拼接，以自己作为起点和终点。

由这个思路就可以构建递推公式了，$D[i]$ 为第 $i$ 个数字作为起点时的最大子数组和，有

$$D[i]=\begin{cases}X[i]+D[i+1]\text{, }D[i+1]>0\\X[i]\text{,}\quad\quad\quad\quad\quad D[i+1]\le0\end{cases}$$

如果需要记录选了哪些数，再开一个 $Rec[i]$ 去记录即可，只需要记录结尾的数就行，如果前面那个点的最大子数组和大于 0，就等于前面那个点对应的结束数字，否则就以自己为结束数字

$$Rec[i]=\begin{cases}Rec[i+1]\text{, }D[i+1]>0\\X[i]\text{,}\quad\quad\quad D[i+1]\le0\end{cases}$$

代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<iostream>
using namespace std;
int num[20010];
int D[20010];
int main(){
    int n;
    int res = -10001;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>num[i];
    }
    for(int i=n;i>0;i--){
        if(D[i]<=0){
            D[i] = num[i];
        }
        else{
            D[i] = D[i+1] + num[i];
        }
        res = max(D[i],res);
    }
    cout<<res<<endl;
}

动态规划解最长公共子序列

例题：

同样是序列问题，考虑起点和终点是否构成递推关系，在这里，我们考虑从前往后枚举终点，就可以递推出前面的。

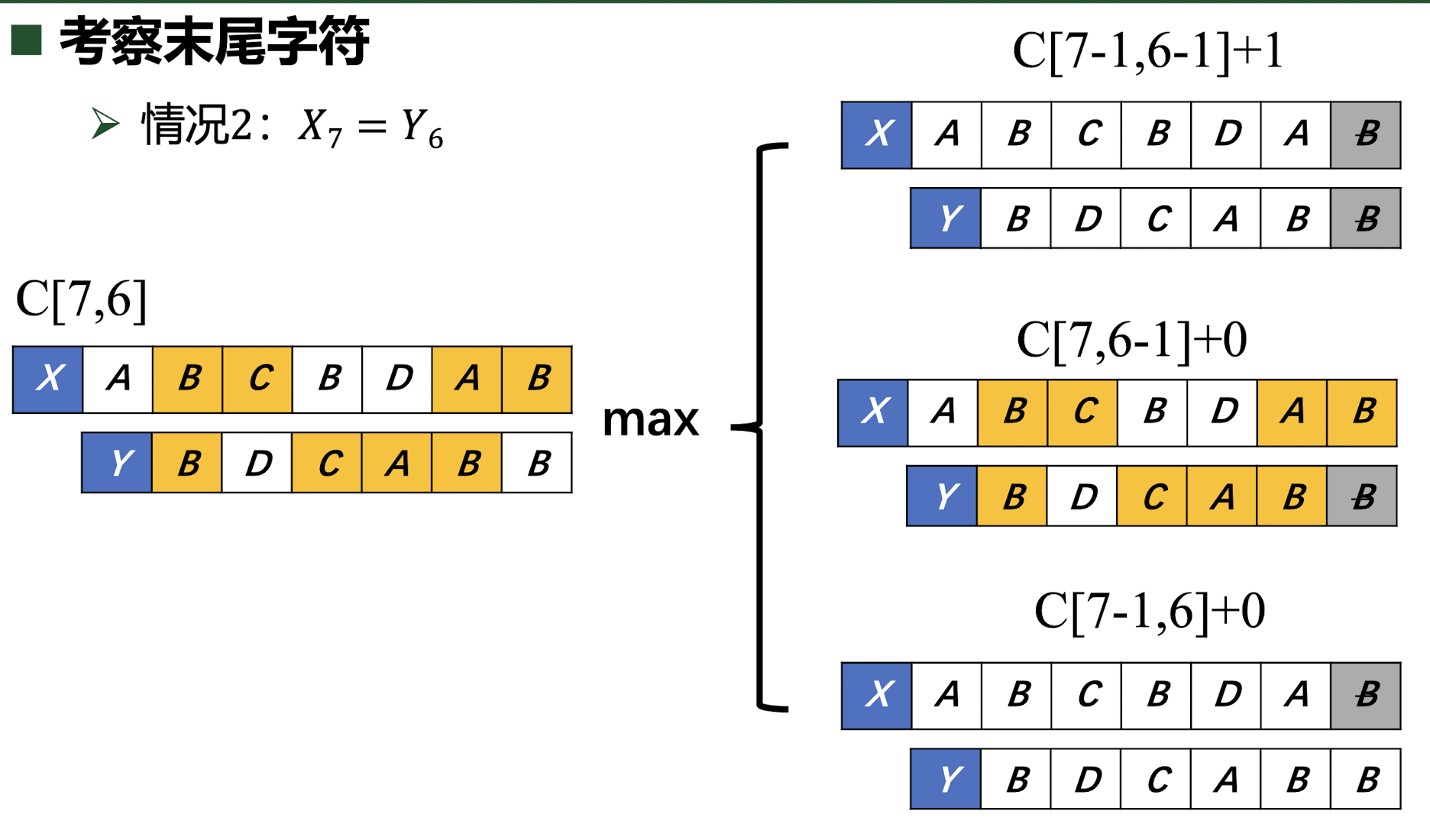
首先对两个对比序列，从终点开始往前匹配，有匹配上了和匹配不上两种情况，对于匹配上了的情况，直接 +1 之后往前递推即可，对于没匹配上的情况，一共有两种走法：

  • 第一个序列往前退一格
  • 第二个序列往前退一格

由于不知道什么情况才能获得最长的序列，我们取 max 进行递推即可。

设$C[i,j]$为遍历到序列 1 第 $i$ 个元素，序列 2 第 $j$ 个元素时的最长公共子序列，递推公式为

$$
C[i,j]=
\begin{cases}
max(C[i-1,j],C[i,j-1]), & \text{if } x_i \not =y_i \\C[i-1,j-1]+1, & \text{if } x_i = y_i
\end{cases}
$$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
#include<vector>
#include<string>
using namespace std;
int main(){
    string str1,str2;
    while(cin>>str1>>str2){
        int n = str1.size();
        int m = str2.size();
        vector<vector<int>> c(n+1,vector<int>(m+1,0));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(str1[i-1]==str2[j-1]){
                    c[i][j] = c[i-1][j-1]+1;
                }
                else{
                    c[i][j] = max(c[i-1][j],c[i][j-1]);
                }
            }
        }
        cout<<c[n][m]<<endl;
    }
    return 0;
}

进阶题：

这道题卡了时间和内存，还要求最长公共子序列的个数。

求最长公共子序列的个数

先看看最长公共子序列的个数怎么求，我们在动态规划的过程中，加入一个 $num$ 数组。

首先来思考什么时候会出现相同的最长公共子序列，只有一种可能，就是在 $c[i-1,j] = c[i,j-1]$
的时候。这个时候由于 $c[i-1,j-1]$ 是确定的，所以可能是字符串 1 多出来的字符和字符串 2
先前的字符匹配上了(或者相反)，对于这种情况

$$ num[i,j] = num[i-1,j] + num[i,j-1] - num[i-1,j-1] $$

由于加多了一部分，就要减去重复的$num[i-1,j-1]$。

对于其他情况，由于不会增加相同的最长公共子序列，就直接令他相等就行了。

以下给一个递推公式（这是课件上的，和我写的递推不一样，但原理是一样的）

$$
num[i,j]=
\begin{cases}
num[i,j]+num[i-1,j-1], & \text{if } x_i=y_j \\num[i,j]+num[i-1,j], & \text{if } x_i\neq y_j \\num[i,j]+num[i,j-1], & \text{if } x_i\neq y_j \\num[i,j]-num[i-1,j-1], & \text{if } x_i\neq y_j \text{ and } \mathsf{C}[i,j]=\mathsf{C}[i-1,j-1]
\end{cases}
$$

内存节约

可以看到内存限制为 $125mb$，我们这边需要开两个二维 $int$ 数组，每个二维数组的大小为 $(5000,5000)$，还要开一个大小为 $5000$ 的一维数组用来存数，总共需要

$$ (5000*5000)*4*2*8/10^6 + 5000*4*8/10^6 \approx 1600mb $$

显然是爆内存了。

仔细观察整个递推过程，起始没必要完全去维护整个表，因为我们只需要最后的结果，而且公式中仅涉及到 $(i-1)～i$ 两个维度的数据，我们开了 $5000$ 个维度，就是浪费，所以这里采用滚动数组去节约内存。

滚动数组示例

滚动数组将 $C[5000][5000],num[5000][5000]$ 化简成 $C[2][5000],num[2][5000]$，然后采用滚动的方式不断去迭代这个 $i$ 和 $i-1$，由于只有两个维度，只涉及到 $0$ 和 $1$的不断变换，这里的滚动方式可以使用异或来进行。

使用滚动数组后，我们计算一下内存

$$ (3*5000)*4*2*8/10^6 + 5000*4*8/10^6 \approx 1.5mb $$

节约了好几倍的内存。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
long MAX = 1e8;
int main(){
    string str1,str2;
    while(cin>>str1>>str2){
        int n = int(str1.size())-1;
        int m = int(str2.size())-1;
        int dp[5001][5001];
        int num[5001][5001];
        for(int i=0;i<=n;i++){
            num[i][0]=1;
        }
        for(int i=0;i<=m;i++){
            num[0][i]=1;
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(str1[i]==str2[j]){
                    dp[i][j] = dp[i-1][j-1]+1;
                    // 如果当前的字符都匹配上了，那么数量一定是不变的
                    num[i][j] += num[i-1][j-1] %MAX;
                }
                else{
                    //如果 y 匹配上了
                    if(dp[i][j]==dp[i-1][j]){
                        num[i][j] += num[i-1][j] %MAX;
                    }
                    //如果 x 匹配上了
                    if(dp[i][j]==dp[i][j-1]){
                        num[i][j] += num[i][j-1] %MAX;
                    }
                    //如果 x 和 y 匹配的字符串相同，那么上面就相当于加了两个相同的字符串，就要减去一份
                    if(dp[i][j]==dp[i-1][j-1]){
                        num[i][j] -= num[i-1][j-1];
                    }
                }
            }
        }
        cout<<dp[n][m]<<endl<<num[n][m]<<endl;
    }
}